technical data Large size conveyor chain Selection

9. How to calculate the tension acting on the chain

The maximum static tension T max acting on the conveyor chain during operation can be calculated from Table 3.

The formula for chain tension T in Table 3 calculates the tension of the entire conveyor based on mass M (weight) x friction coefficient.

Inertial forces become very large when a high-speed conveyor starts or stops suddenly, or when a pusher conveyor moves conveyed items suddenly. In such cases, calculate the chain tension and required power taking inertial forces into consideration.

The formula is written in both SI units and gravity units. When calculating tension T in gravity units, weight (kgf) in gravity units is the same value as mass (kg) in SI units.

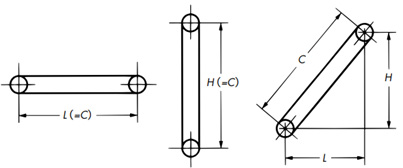
Tension acting on the chain

9.1 Explanation of Terms

SI units Gravity Units
TMAX Maximum static tension acting on the chain kN {kgf}
T'MAX Correction chain tension kN {kgf}
T Static tension acting on the chain kN {kgf}
Q Maximum possible transport volume t/h {tf/h}
V Conveying speed (chain speed) m/min m/min
H Sprocket center distance (vertical direction) m m
L Sprocket center distance (horizontal direction) m m
C Sprocket center distance m m
M Mass of the moving part {weight}
(Chain x number of strands, mass {weight} of bucket, apron, etc.)		 kg/m {kgf/m}
f1 Friction coefficient between chain and guide channel (Table 5, Table 6)
f2 Coefficient of sliding friction between the transported object and the bottom and side plates (Table 7)
f When directly loaded, f=1 When scraping, f=f2/f1
g Gravitational acceleration 9.80665m/s 2
W Amount of material transported {weight}
bulk item
W=16.7 * ×Q/V {W=16.7*×Q/V}
countable item
W = Amount of material being transported (kg/piece) / Loading interval (m)
{W = Weight of transported item (kgf/item) / Loading interval (m)}		 kg/m {kgf/m}

Note: The coefficient used to convert the mass (weight) of bulk item per meter of chain is 16.7 = 1000/60

*If forward and reverse operation is performed frequently, the chain will need to be taken up by take-up, so the calculation formula will differ from the one below.
If you are taking up slack in the chain with a take-up, please use the calculation formula in Q&A6 here.

9.2 Chain tension calculation (Table 3)

SI units {gravity unit}

Horizontal transport

Horizontal transport

T1 = 1.35 ※1 × M × L1 × g 1000 ......kN

T2 = ( L - L1) × M × f1 × g 1000 + T1 ......kN

T3 = 1.1 ※2 × T2 ......kN

TMAX = (W × f + M ) × L × f1 × g 1000 + T3 ......kN

T1 = 1.35 × M × L1 ......{kgf}

T2 = ( L - L1) × M × f1 + T1 ......{kgf}

T3 = 1.1 × T2 ......{kgf}

TMAX = (W × f + M ) × L × f1 + T3 ......{kgf}

  • *1 See Table 4 below
  • *2 1.1 is the tension increase coefficient at the driven sprocket

Horizontal transport

Horizontal transport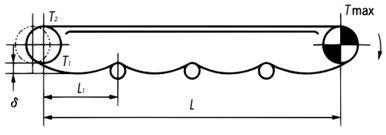

T1 = 1.35 × M × L1× g 1000 + 0.1※ × M × L × g 1000 ......kN

T2 = 1.1 × T1 ......kN

TMAX = (W × f + M) × L × f1 × g 1000 + T2 ......kN

T1 = 1.35 × M × L1 + 0.1※ × M × L ......{kgf}

T2 = 1.1 × T1 ......{kgf}

TMAX = (W × f + M) × L × f1 ......{kgf}

  • *0.1 is the rotational resistance coefficient of return-way roller

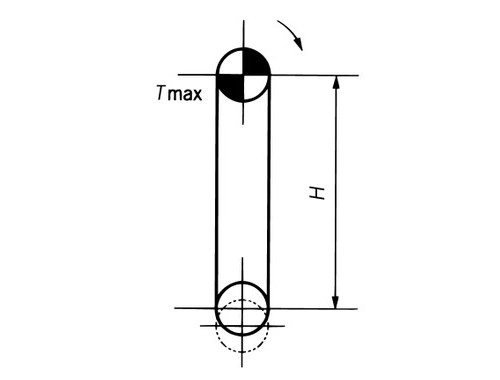
Vertical Conveyance

Vertical Conveyance
  • Note: For bucket elevators, the sprocket center distance (H) is calculated by adding 1 m to account for the increased load when loading transported items.
    W T: Take-up load. Due to the pulley principle, half of the take-up load acts on each chain.

TMAX = (W + M) × H × g 1000 + WT 2 × g 1000 ......kN

TMAX = (W + M) × H + WT 2 ......{kgf}

Inclined conveyance

Inclined conveyance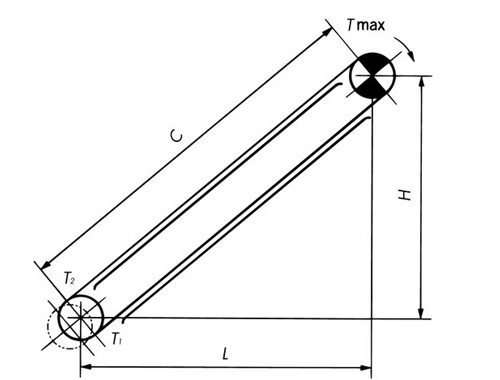

T1 = M(Lf1 - H) × g 1000 ......kN

If T 1 < 0, then T 2 = 0

T2 = 1.1 × T1 ......kN

TMAX = W(Lf1 × f + H) × g 1000 + M(Lf1 + H) × g 1000 + T2 ......kN

T1 = M(Lf1 - H) ......{kgf}

If T 1 < 0, then T 2 = 0

T2 = 1.1 × T1 ......{kgf}

TMAX = W(Lf1 × f + H) + M(Lf1 + H) + T2 ......{kgf}

Application Examples

Application Examples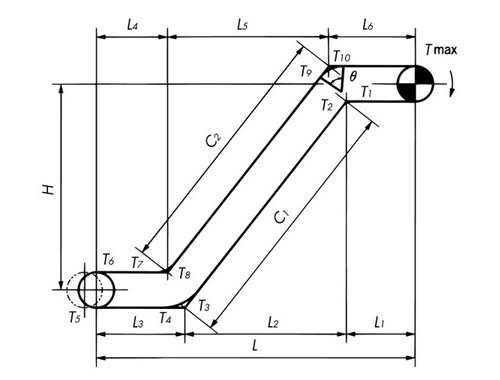

T1= M × L1 × f1 × g 1000 ......kN

T2= T1× Kc1 ......kN

T3= M(L2f1 - H) × g 1000 + T2 ......kN

T4= T3× Kc2 ......kN

If T 3 < 0, then T 4 = 0

T5= M × L3 × f1 × g 1000 + T4 ......kN

T6= 1.1 × T5 ......kN

T7= (M + W × f) × L4 × f1 × g 1000 + T6 ......kN

T8= T7× Kc3 ......kN

T9= W(L5f1 × f + H) × g 1000 + M(L5f1 + H) × g 1000 + T8 ......kN

T10 = T9× Kc4 ......kN

TMAX = (M + W × f) × L6 × f1 × g 1000 + T10 ......kN

Corner coefficient Kc

f1 angle
30° 60° 90° 120° 180°
0.03 1.02 1.03 1.05 1.06 1.10
0.10 1.05 1.11 1.17 1.23 1.37
0.15 1.08 1.17 1.27 1.37 1.60
0.20 1.11 1.23 1.37 1.52 1.87
0.24 1.13 1.29 1.46 1.65 2.13
0.30 1.17 1.37 1.60 1.87 2.57
0.40 1.23 1.52 1.87 2.31 3.51

T1 = M × L1 × f1 ......{kgf}

T2 = T1 × Kc1 ......{kgf}

T3 = M(L2f1 - H) + T2 ......{kgf}

T4 = T3 × Kc2 ......{kgf}

If T 3 < 0, then T 4 = 0

T5 = M × L3 × f1 + T4 ......{kgf}

T6 = 1.1 × T5 ......{kgf}

T7 = (M + W × f) × L4 × f1 + T6 ......{kgf}

T8 = T7 × Kc3 ......{kgf}

T9 = W(L5f1 × f + H) + M(L5f1 + H) + T8 ......{kgf}

T10 = T9 × Kc4 ......{kgf}

TMAX = (M + W × f) × L6 × f1 + T10 ......{kgf}

Example of Double Plus Free Flow Chains

Example of Double Plus Free Flow Chains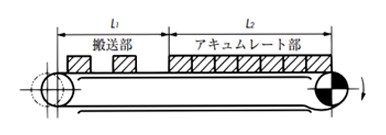

TMAX = 2.1M(L1 + L2) f1 × g 1000 + (W × L1 × f1)
× g 1000 + (W1 × L2 × f3 × g 1000 ) ......kN

TMAX = 2.1M(L1 + L2) f1 + (W × L1 × f1) + (W1 × L2 × f3) ......{kgf}

  • L 1: Length of conveying section (m)
  • ​L2: Length of the accumulation section
  • W 1: Amount of material conveyed in the accumulator (kg/m) {mass kgf/m}
  • f 1: Friction coefficient between chain and rail during transport (0.05)
  • ​f3: Friction coefficient during accumulation (0.2)

The chain tension T used to calculate the required power is given by the following formula.

Horizontal T = T MAX- T 1

Vertical T = T MAX- MH × g 1000

Slope T = T MAX- M(H - Lf 1) × g 1000

T = TMAX - MH

T = TMAX - M(H - Lf1)

  • When H - Lf 1 is negative, T = T MAX.

・Calculation of required power

1kW = 1kN・m/s

kW = T × V 60

1kW = 102kgf・m/s

kW = T × V 102 × 60

Power loss due to the meshing of the chain and sprocket, and the frictional resistance of the sprocket's rotation, is considered to be about 10% (1/0.9 = 1.1).

If the transmission mechanical efficiency of the drive unit is η, then

kW = T × V 60 × 1.1 × 1 η

kW = T × V 102 × 60 × 1.1 × 1 η

Table 4. Catenary tension graph

カテナリ張力グラフ

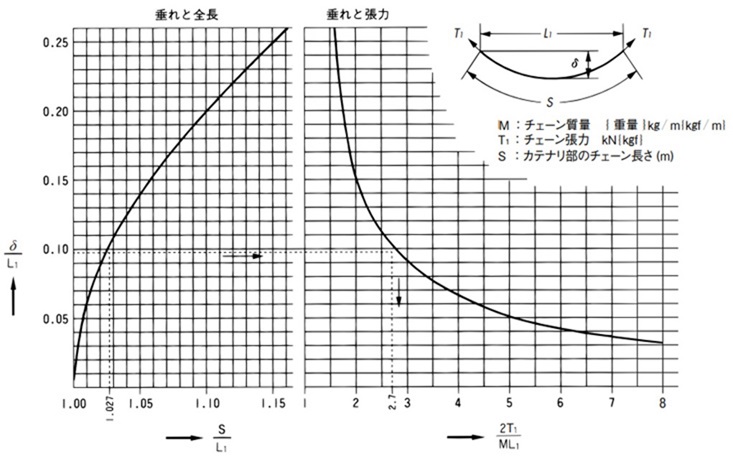
How to calculate catenary tension

T1 = 1.35 × M × L1 × g 1000 ......kN

1.35 in this formula is:

When the catenary volume is 10%, δ = 0.10L 1

From the above figure
δ L 1 = 0.10 → 2T 1 ML 1 = 2.7
T 1 = 1.35 × M × L 1 × g 1000

How to determine the length of the catenary chain

δ L1 = 0.10 → S L1 = 1.027

S = 1.027L1

Table 5. Rolling friction coefficient between chain and guide channel (room temperature) f 1

Roller diameter classification
(mm)		 Lubrication condition When the lubricant runs out
R, F roller S, M, N roller R, F roller S, M, N roller
D＜65 0.08 0.16 0.15 0.24
65≦D＜100 0.08 0.15 0.14 0.23
100≦D 0.08 0.14 0.13 0.22
RF-214 (Exception) 0.12 0.15 0.18 0.22

Note)

  • 1. When lubricating with ISO VG100-150 (SAE30-40)
  • 2. Indoor atmosphere with little dust and room temperature
  • 3. The top roller of the chain with top rollers and f1 of the conveyed object are the same as those of the R rollers above.
series f1
Plastic Roller Series 0.08 (Lube-free)
Bearing Roller Series 0.03 (lubricated)
Needle bushing series 0.14 (lubricated), 0.21 (out of lubricant)
EPC78 0.1 (lubricated), 0.2 (water lubrication), 0.25 (lack of lubricant)

Table 6. Coefficient of friction between chain and guide channel f1

Temperature of transported goods ℃ Lubrication condition Out of lubricant
Room temperature to 400 0.20 0.30
400～600 0.30 0.35
600～800 0.35 0.40
800～1000 - 0.45

Table 7. Coefficient of friction f2 between the conveyed object and the bottom and side plates

Transported goods f2 Apparent specific gravity
scale 0.67 1.54
Hematite 0.47 2.99
pyrite 0.58 1.54
iron slag 0.48 0.90
scrap 0.73 0.54
lead ore powder 0.77 3.26
zinc ore powder 0.79 1.93
Nickel Ore Powder 0.45 0.92
Chromium ore powder 0.51 1.14
alumina 0.55 0.83
Magnesia 0.84 1.48
gypsum 0.64 0.77
quartz powder 0.55 1.24
feldspar 0.55 1.36
Dolomite 0.55 1.62
clay 0.63 0.77
Foundry sand 0.41 1.59
phosphate rock 0.42 1.51
quicklime 0.46 1.53
slaked lime 0.63 0.69
asbestos 0.58 0.19
limestone 0.47 0.35～0.55
cement 0.54 0.60～0.75
cement clinker 0.46 1.30
charcoal 0.41 0.44
carbon 0.53 0.30
Pitch 0.41 0.70
Soda ash 0.45 0.52
Alum 0.63 1.01
polyethylene 0.52 0.34
rubber powder 0.53 0.39
Soap ingredients 0.27 0.65
urea 0.63 0.64
ammonium chloride 0.79 0.67
calcium chloride 0.43 0.68
calcium sulfide 0.64 1.01
calcium carbonate 0.49 0.88
wood chips 0.74 0.36
rice 0.4 0.77
barley 0.71 0.39
wheat 0.43 0.73
soy 0.41 0.68
corn 0.4 0.71
starch 0.57 0.71
sugar 0.47 0.68
rock salt 0.57 1.09
mixed feed 0.5 0.55
coal - 0.30～0.70
Coke - 0.30～0.70

Note: The above values may change depending on the humidity and dryness.

Return to determining attachment format

Return to Table of Contents

Proceed to chain size determination