1. Chain length (number of links): L
Winding transmission

When using a two-shaft winding transmission

• (1) When the center distance and number of teeth of both sprockets are fixed

  L = Z + Z' 2 + 2C + Z - Z' 6.28 ² C
  

• (2) When the number of chain links and teeth is fixed
  C = 1 8   2L - Z - Z' + (2L - Z - Z')² - 8 9.86 (Z - Z')²
  Any fractional part (decimal part) of the calculated L value will be rounded up and counted as one link, even if it is small.
  If there is an odd number of links, an offset link must be used, but if possible, change the number of sprocket teeth or the center distance to make it an even number of links.

Pin gear drive

When using a chain with an attachment wound around the outside of the drum

L = 180° tan^-1 P D + 2S

• P: Chain pitch
• D: Drum outer diameter
• S: Attachment height

• * Round L up to an even number of links.
• * When installing the chain attachment on the outside of the drum, insert shims evenly to adjust the fit.

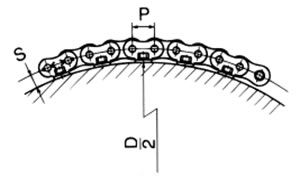
2. Chain speed: V

V = P × Z' × n 1000 (m/min)

3. Chain tension at rated motor output (kW) and rated rotation speed: Fm

Fm = 60 × kW V (kN)

Fm = 6120 × kW V (kgf)

4. Load moment of inertia I(GD ²)of
Converted to prime mover shaft
Moment of inertia: I _ℓ (GD ²_ℓ)

I_ℓ = M × V 2πn₁ ² (kg・m²)

GD²_ℓ = W × V πn₁ ² (kgf・m²)

5. Rated torque of the prime mover: Tn

Tn = 9.55 × kW n₁ (kN・m)

Tn = 974 × kW n₁ (kgf・m)

6. Working torque: Tm

Tm = Ts(%) + T _max (%) 2 × 100 × Tn (kN・m)
or
Tm = Ts(kN・m) + T _max (kN・m) 2 (kN・m)

Tm = Ts(%) + T _max (%) 2 × 100 × Tn (kgf・m)
or
Tm = Ts(kgf・m) + T _max (kgf・m) 2 (kgf・m)

7. Chain tension due to starting torque: Fms

Fms = Ts(%) × i {d/(2 × 1000)} × 100 × Tn × 1(kN)
or
Fms = Ts(kN・m) × i d/(2 × 1000) × 1(kN)

Fms = Ts(%) × i {d/(2 × 1000)} × 100 × Tn × 1(kgf)
or
Fms = Ts(kgf・m) × i d/(2 × 1000) × 1(kgf)

Chain tension due to brake torque: Fms

Fmb = T _b (%) × i {d/(2 × 1000)} × 100 × Tn × 1.2*(kN)
or
Fmb = T _b (kN・m) × i d/(2 × 1000) × 1.2*(kN)

* is a constant

Fmb = T _b (%) × i {d/(2 × 1000)} × 100 × Tn × 1.2*(kgf)
or
Fmb = T _b (kgf・m) × i d/(2 × 1000) × 1.2*(kgf)

* is a constant

8. Acceleration time: ts
If the acceleration time is known, use that time.

ts = (Im + I_ℓ) × n₁ 9550 × (Tm - T_ℓ) (s)

ts = (GD²m + GD²_ℓ) × n₁ 375 × (Tm - T_ℓ) (s)

9. Deceleration time: t _b
If the deceleration time is known, use that time.

±: For negative loads such as hanging loads
Let's say -T _ℓ.

t_b = (Im + I_ℓ) × n₁ 9550 × (Tb ± T_ℓ) (s)

t_b = (GD²m + GD²_ℓ) × n₁ 375 × (Tb ± T_ℓ) (s)

10. Acceleration

• Linear motion: αs
• Rotational motion: ωs

Assumes straight line acceleration.

If not, calculate at maximum acceleration.

Linear motion (load acceleration) αs = V _ℓ ts × 60

Rotational motion (angular velocity of the prime mover shaft) ω = 2 π × n1

Rotational motion (angular acceleration of the prime mover shaft) ωs = ωts × 60

11. Deceleration

• Linear motion: αb
• Rotational motion: ωb

Assumes straight line acceleration.

If not, calculate at maximum deceleration.

Linear motion (load deceleration) αb = V _ℓ tb × 60

Rotational motion (angular velocity of the prime mover shaft) ω = 2 π × n1

Rotational motion (angular deceleration of the prime mover shaft) ωb = ωtb × 60

12. Chain tension during acceleration: Fs

Linear motion Fs = M × αs 1000 + Fw

Rotational motion Fs = I _ℓ × ωs × i 1000 × d 2 × 1000 + Fw

Linear motion Fs = M × αs G + Fw

Rotational motion Fs = GD ²_ℓ /4 × ωs × i d 2 × 1000 × G + Fw

Chain tension during deceleration: Fb

Linear motion Fb = M × αb 1000 + Fw

Rotational motion Fb = I _ℓ × ωb × i 1000 × d 2 × 1000 + Fw

Linear motion Fb = M × αb G + Fw

Rotational motion Fb = GD ²_ℓ /4 × ωb × i d 2 × 1000 × G + Fw

13. Correction kW (for general selection)

14. Compensation chain tension

Correction chain tension from the prime mover: F'm

Corrected chain tension from starting torque: F'ms

Correction chain tension from stall torque: F'mb

Compensation chain tension of the carriage drive: F'c

Corrected chain tension during acceleration: F's

Corrected chain tension during deceleration: F'b

Corrected chain tension from load: F'w

F'w = M × Ks × Kn × Kz × G 1000 (kN)

F′w = W (or Fw) × Ks × Kn × Kz (kgf)

If the mass M {weight W} is unknown, calculate the shaft torque T = Tn × i (kN・m) {kgf・m} from the rated torque Tn of the prime mover,
Instead of W, use F = 2T/d.

15. Inertia ratio: R

R = I_ℓ Im

R = GD²_ℓ GD²m

16. Conversion of moment of inertia (I) and flywheel effect (GD ²)